دنیای زبان انگلیسی ( بهروزپور )
لغات و اصطلاح .داستان کوتاه . شعر.جوک .ضرب المثل.اشپزی.رمان. نمایشنامه.متن دوزبانهدنیای زبان انگلیسی ( بهروزپور )
لغات و اصطلاح .داستان کوتاه . شعر.جوک .ضرب المثل.اشپزی.رمان. نمایشنامه.متن دوزبانهروزانهها
همه- queen.blogfa.com
- وبلاگ زبان انگلیسی دبیرستان سمپاد ملایر
- Join to English
- *´`·.. • • • POEM • • •..·´`*
- rasol academy
- poem
- آموزش زبان انگلیسی
- تدریس و ترجمه کلیه زبانها
- دهکده انگلیسی
- یادداشتهای هماره
- دانشجویان زبان انگلیسی
- شهرزبان
- دبیری زبان دانشگاه فرهنگیان
- English Barobax
- دنیای زبان من: آموزش زبان های خارجه
- وبلاگ آی زبان
- موفقیت من و تو در یادگیری زبان اموزش زبان
- خاطرات خاله نرگس
- دیدنی ها
- English village
- Language Garden
- وبلاگ پرویز ولد خانی
- سایه روشن
- اموزش زبان انگلیسی البیون
- جهان آموزش
- بهترین سایت آموزش انگلیسی رایگان و بزرگترین انجمن ایرانیان علاقه مند به انگلیسی
- خیابان انگلیسی
- آموزش زبان انگلیسی و فرانسه
- کتاب الکترونیکی زبان من /بهروزپور
- بغض چشم
- اموزش زبان انگلیسی دیالوگ
- زبان شناس آینده
- کتابخانه مجازی اموزش زبان لایبر
- love
- ترجمه انگلیسی قران
- An English Translator
- موفقیت من و تو در یادگیری زبان اموزش زبان
- مجموعه کتابهای الکترونیکی دانش و زندگی/رضا فریدون نژاد
- تخصصی کارشناسی ارشد ادبیات فارسی
- وبلاگ سمیرحسین نژاد
- نماز و نیایش
- مترجمی زبان انگلیسی - پیام نور اهواز
- وبلاگ ali rahimian
- در این وبلاک از جون آدمی زاد تا شیر مر غ می توان یافت
- دنیای زبان انگلیسی(رضایی)
- کالج زبان چهار دانگه
- Where a rainbow of our ideas is formed
- engelisi baraye jahane emrooz
- آموزش نرم افزار CATIA
- ترجمه انگلیسی قران
پیوندها
- معما
- شعر
- گرامر
- دیباچه
- fiction
- poetry
- poems
- کتاب نیوز
- دیکشنری
- کتاب سبز
- ازمون تافل
- تاریخ فلسفه
- Food Idioms
- نمایشنامه ها
- sms انگلیسی
- کتابهای صوتی
- تبیان انگلیسی
- Literary Terms
- اصطلاحات ادبی
- اشعار انگلیسی
- ادبیات انگلیسی
- دیکشنری انلاین
- ادبیات انگلیسی
- اموزش انگلیسی
- دنیای ضرب المثل
- تمام اثار شکسپیر
- یادگیری انگلیسی
- دیکشنری تصویری
- دیکشنری تصویری
- business writing
- اشپزی (انگلیسی)
- 180 شعر انگلیسی
- دانلودکتابهای صوتی
- رسم الخط انگلیسی
- آموزش گرامر تصویری
- مکالمه های انگلیسی
- انگلیسی برای کودکان
- سایت سهراب سپهری
- The Quotations Page
- نویسندگان مشهور جهان
- دیکشنری تصویری اینترنتی
- توانایی های ضروری زندگی
- صدهاداستان (متن و صوت)
- نقل قول های زیبای تصویری
- سایتی برای متنهای دو زبانه
- سایت اسلامی به انگلیسی
- شعر انگلیسی برای کودکان
- دانلود رایگان رمانهای خارجی
- راهنمای انگلیسی (تصویری)
- Middle Ages (ارشیو صوتی)
- داستانهای کوتاه برای کودکان
- جدول های انگلیسی با جواب
- یادگیری اسان لغات انگلیسی
- اصطلاح وضرب المثل با تصاویر
- کتابخانه الکترونیکی مای بوک
- تصویری grammarmindmaps
- سایت اصطلاح های انگلیسی
- دانلود رمانها .شعر. داستان کوتاه
- اصطلاح. لغت. ضرب المثل و گرامر
- اصطلاحات مربوط به داستان کوتاه
- دانلود بهترین اثار نویسندگان حارجی
- همه چی در مورد یادگیری انگلیسی
- Popular Contemporary Poetry:شعر
- معما/ چیستان / پازل و ....به انگلیسی
- your best quotes, jokes, and sayings
- Idioms and Sayings About The Human Body
دستهها
- شعر / شعرهای دو زبانه/اهنگ 99
- رمان انگلیسی 32
- مکتبهای ادبی / نقد ادبی 16
- شخصیتهای ادبی 29
- نمایشنامه 15
- اصطلاحات ادبی انگلیسی 11
- ضرب المثل/اصطلاح .مخفف 72
- اس ام اس/ نقل قول /معما/جوک 214
- ایران /مکانهای دیدنی ایران 19
- ارشد زبان/تافل /اموزش گرامر زبان 66
- خواندنیها 75
- اشپزی/تغذیه/سلامتی 69
- دیکشنری ها /مجلات 9
- تصاویر متن دار انگلیسی 318
- داستان /داستان کوتاه دو زبانه 151
- اصطلاح و ضرب المثل (تصویری) 39
- اموزش تصویری لغات , افعال 79
- مذهبی 36
- اموزش نامه نگاری/ مسایل روزمره 7
- تاریخ ادبیات انگلیسی 4
- متن های زیبا فارسی 12
- کتابهای الکترونیکی من 28
جدیدترین یادداشتها
همه- shallکاربرد
- کاربرد صحیح مکالمات انگلیسی
- اصطلاحات معمول انگلیسی :
- life
- think
- ضرب المثل
- شعر
- A boat I will shape:قایقی خواهم ساخت:سهراب سپهری
- داستان کوتاه جان و ساعت ( فارسی و انگلیسی )
- نکات جالب و عجیب اعداد و حروف انگلیسی
- بهترین لحظات زندگی از نگاه چارلی جاپلین
- ضرب المثل/ اصطلاح
- Ah! Sunflower
- life
- h/g
- 50 Ways To Be Happier
- اصطلاح dead meat
- خداوند در زبان انگلیسی
- life..........
- Happy Ramadan
- fact of life
- (:
- داستان کوتاه انگلیسی همراه با ترجمه فارسی (عشق و زمان)
- زیباترین جملات
- 30 ضرب المثل انگلیسی با معنی فارسی
- HAPPY BIRTHDAY IMAM MAHDI
- 15th Shaban
- imagine
بایگانی
- بهمن 1394 2
- تیر 1394 5
- مهر 1393 6
- مرداد 1393 6
- تیر 1393 6
- خرداد 1393 8
- اردیبهشت 1393 9
- فروردین 1393 8
- اسفند 1392 13
- بهمن 1392 5
- دی 1392 6
- آذر 1392 9
- آبان 1392 16
- مهر 1392 23
- شهریور 1392 51
- مرداد 1392 59
- تیر 1392 40
- خرداد 1392 44
- اردیبهشت 1392 47
- فروردین 1392 20
- اسفند 1391 49
- بهمن 1391 65
- دی 1391 41
- آذر 1391 37
- آبان 1391 21
- مهر 1391 18
- شهریور 1391 5
- مرداد 1391 2
- تیر 1391 11
- خرداد 1391 3
- اردیبهشت 1391 6
- فروردین 1391 3
- اسفند 1390 6
- بهمن 1390 8
- دی 1390 8
- آذر 1390 8
- آبان 1390 7
- مهر 1390 11
- شهریور 1390 9
- مرداد 1390 15
- تیر 1390 23
- خرداد 1390 25
- اردیبهشت 1390 54
- فروردین 1390 67
- اسفند 1389 87
- بهمن 1389 257
- دی 1389 148
تقویم
بهمن 1394| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
آمار : 956061 بازدید
Powered by Blogsky
معما
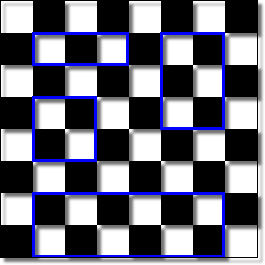
How many squares are there on a chessboard?? (the answer is not 64)
Can you extend your technique to  calculate the number of rectangles on a chessboard
calculate the number of rectangles on a chessboard
This another puzzle that was also e-mailed to me through this website. My instinct was that the answer was just a lot, but i thought about it and the solution is actually fairly simple...
Can you extend your technique to calculate the number of rectangles on a chessboard?The first thing is why the answer is not just 64...
All the red squares in the above picture would count as valid squares, so we are asking how many squares of any dimension from 1x1 to 8x8 there are on a chess board.
The key is to think how many positions there are that each size of square can be located...
A 2x2 square, for example, can be located in 7 loactions horizontally and 7 locations vertically. ie in 49 different positions. Consider the table below...
size horizontal positions vertical positions positons 1x1 8 8 64 2x2 7 7 49 3x3 6 6 36 4x4 5 5 25 5x5 4 4 16 6x6 3 3 9 7x7 2 2 4 8x8 1 1 1 total 204
In total there are 204 positions. this is the sum of the number of possible positions for all the different sized squares.
Below are some examples of possible rectangles...
All of the above examples would be vailid rectanges...
The key to this problem is to think of each rectangle individually and consider the number of positions it can be located. For example a 3x7 rectangle can be located in 6 positions horizontally and 2 vertically. From this we can build a matrix of all the possible rectangles and sum.
dimesions 1 2 3 4 5 6 7 8 positions 8 7 6 5 4 3 2 1 1 8 64 56 48 40 32 24 16 8 2 7 56 49 42 35 28 21 14 7 3 6 48 42 36 30 24 18 12 6 4 5 40 35 30 25 20 15 10 5 5 4 32 28 24 20 16 12 8 4 6 3 24 21 18 15 12 9 6 3 7 2 16 14 12 10 8 6 4 2 8 1 8 7 6 5 4 3 2 1 1296 In total then there are 1296 possible rectangles.
http://puzzles.nigelcoldwell.co.uk/twentyseven.htm