معما

You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner

(the one farthest from you). Describe the sh

ortest path that you can walk

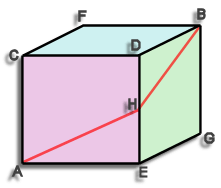
Answer to Puzzle #3: The Fly in a Cubic Room

You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner (the one farthest from you). Describe the shortest path that you can walk.

I worked this one out for myself so it clearly isn't that hard...

First consider the diagram:-

ش

The problem phrased differently is that we have to get from point A to point B only moving along the walls.

The shortest route is shown it is A-H-B where H is the mid point of D-E.

The length of this route can easily be calculated, assume the cube has sides of length 1 unit (it doesn't matter what these units are, meters, feet, what ever) The distance A-H is the hypotenuse of a triangle 1 x ½ a quick bit of pythag tells us that A-H equals sqrt(5/4). Similarly H-B has the same length hence the total length is 2 x sqrt(5/4) this is actually equal to the square root of 5

A-H-B = sqrt(5) = 2.236

Some people think the shortest root is A-C-B or A-E-B or A-F-B etc. (they are all the same) this has a length of 1 + sqrt(2) ie. about 2.414

http://puzzles.nigelcoldwell.co.uk/three.htm

.